
Tout d'abord, voici ce qu'il faut savoir pour continuer  :
:
I. Définition de la fonction exponentielle (tiré d'une fiche d'Ilemaths):
Il existe une unique fonction f, dérivable sur R, telle que f' = f et f(0) = 1. On la nomme fonction exponentielle : elle sera notée exp.
Conséquences:
- exp(0) = 1
- exp est dérivable sur R et exp'(x) = exp(x)
- pour tout réel x, exp(x) > 0
- la fonction exp est strictement croissante sur R
Définition de la fonction logarithme népérien :
La fonction logarithme Népérien, notée ln, est la bijection réciproque de la fonction exp :
Pour tout x de]0 ; + l'infini[ et tout y de R, ln(x) = y équivaut e^y = x .
Propriétés algébriques dont nous nous sommes servies :
Pour tous x et y de ]0 ; +infini[ et tout entier n :
ln(xy) = ln(x)+ln(y), ln (e^x) = x et ln(x^n) = nln(x) .
Nous souhaitions aborder quelques notions mathématiques. Pour ce faire nous avons utilisé une des courbes qui s'approcher le plus de la théorie : la courbe représentant l'évolution des bactéries dans le morceau témoin mis à température ambiante.
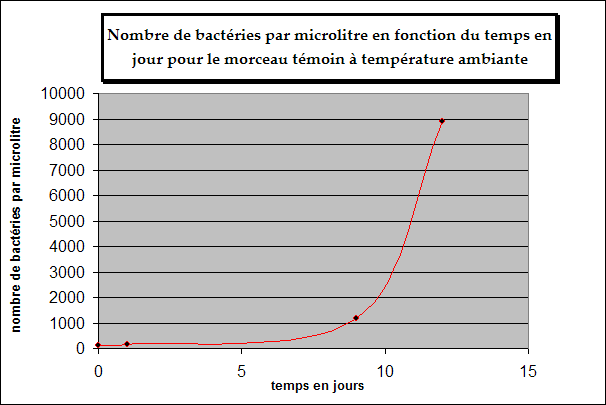
D'après nos connaissances, nous savions que les bactéries se divisaient exponentiellement car il y avait division cellulaire. Nous avons donc voulu trouver la courbe de tendance exponentielle de cette courbe.
Nous avons fini par trouver une équation qui est : m(x)= 105.4739445e^0.333978457x
Mais comment avons nous fait?
Tout d'abord, nous avons posé Y=ln(y).
Nous avions donc un tout autre tableau de résultat qui est:

Or on suppose ensuite que la courbe a une allure exponentielle, c’est-à-dire que, m(x) =k.e^px avec Cm qui est la courbe de tendance.
Grâce à la calculatrice (nous avons entré notre liste puis demandé la droite de régression appélé Linreg(ax+b) pour les TI) nous avons trouvé l'équation de la droite de régression:
Y= ax+b avec a= 0.333978457 b=4.658463951

De plus:
On a Y= ln(y)= ln(k.e^px) = ln(k)+ pxln(e) = px+ln(k)
On sait que Y = px + ln(k) et que Y = 0.333978457x + 4.658463951
Donc par identification: p = 0.333978457 et ln(k)= 4.658463951
soit k= e^ 4.658463951 = 105.4739445
Donc la courbe de tendance exponentielle a pour équation:
m(x)= 105.4739445e^0.333978457x

Par la suite, nous nous sommes rendues compte que leur croissance n'avait pas entièrement une allure exponentielle  . En effet, seule une partie de cette croissance l'est.
. En effet, seule une partie de cette croissance l'est.

Légende:
- 1 : phase de latence
- 2 : phase d'accélération
- 3 : phase exponentielle
- 4 : phase de ralentissement
- 5 : phase stationnaire
- 6 : phase éventuelle de mortalité.
On peut donc penser que notre phase exponentielle ne se situe qu'entre t9 et t12 sur notre graphique. Nous avons donc recommencé pour trouver l'équation qui serait la réelle équation exponentielle de la phase 3.

Nous sommes donc arrivé à cette courbe  :
:

Si cette courbe de tendance parait si parfaite, c'est tout simplement car nous n'avions que deux points afin de trouver son équation.